Zusammenhang zwischen scheinbaren Restextrakt und tatsächlichen Restextrakt

[christianf]

Hallo zusammen,

ich versuche gerade die verschiedenen Formeln ums Brauen zu verstehen und die meisten lassen sich ja auch aus einfachen physikalischen Zusammenhängen elementar ableiten. Beim Zusammenhang zwischen dem scheinbaren Restextrakt und dem tatsächlichen Restextrakt stecke ich allerdings fest.

Die Formel für den tatsächlichen Restextrakt, die überall mitgeteilt, aber nie begründet wird, lautet (***)

Er = 0,8192 · Es + 0,1808 · Eo

(E steht bei mir für Extrakt und die Indizes r für "Rest", s für "scheinbar" und o für "original", also für die Stammwürze.)

Die beiden Koeffiezient 0,8192 und 0,1808 addieren sich zu 1, der tatsächliche Restextrakt Er wird also quasi aus 81,92% vom scheinbaren Restextrakt Es und 18,08% vom originalen Extrakt Eo (also der Stammwürze) zusammengemixt. Aber wie kommen diese beiden Koeffizienten zustande?

Für sicher halte ich, dass die sogenannte Balling-Näherung (*) eine Rolle spielt, die einen Zusammenhang zwischen Stammwürze, Alkohol und tatsächlichem Restextrakt herstellt:

Eo = 2,0665 · A + Er

Das ist einfach eine Bilanzgleichung, in der drin steckt, dass man 2,0665 g vergärbaren Zucker braucht, um 1 g Alkohol zu bekommen. Die ursprüngliche Stammwürze Eo muss also die Summe aus diesem vergorenem Zucker (2,0665 · A) und dem unvergorenem Extrakt Er sein. (*)

Sicher spielt auch noch die Dichte von Alkohol 0,7893 g·cm−3 (20 °C) eine Rolle, denn es ist ja gerade diese geringere Dichte, die den sogenannten Alkoholfehler bei der Spindel-Ablesung verursacht.

Wahrscheinlich spielt auch noch die Tabarié-Gleichung(**) eine Rolle.

Aber wie ich das alles jetzt zusammenbauen muss, da stehe ich gerade auf dem Schlauch

Vielleicht hat einer von euch eine Idee oder hat die Herleitung mal irgendwo gesehen.

(*) In der genaueren Balling-Formel steckt auch noch drin, dass ein kleines bisschen Masse durch CO2 und Hefe verloren geht, aber das dürfte bei dieser Ableitung keine Rolle spielen.
(**) Die Tabarié-Gleichung besagt, dass die Dichteänderungen von Zucker und Alkohol gegenüber reinem Wasser sich addieren.
(***) Bei Sandro TRE = 0,1808 · Stammwürze[°P] + 0,8192 · SRE[°P] , aber ich finde meine Schreibweise übersichtlicher

Edit: Kleinere Aufräumarbeiten und (**) ergänzt

[olibaer]

Servus Christian,

...ich versuche gerade die verschiedenen Formeln ums Brauen zu verstehen
Die Formel für den tatsächlichen Restextrakt, die überall mitgeteilt, aber nie begründet wird, lautet (***)

Er = 0,8192 · Es + 0,1808 · Eo

Ja, ein Formular-Overload.
Gerne kopiert, gerne verwendet aber selten verstanden und hinterfragt. Eine Entsprechung für

Ew = 0,8192 x Es + 0,1808 x P

findet sich wesentlich durchsichtiger dargestellt im Formelwerk:

Ew = P - (P - Es) x 0,8192

Hier zumindest kommt die von Balling beschriebene Attenuationsdifferenz zum Vorschein. Zitat:
"Die scheinbare Attenuation ist immer größer als die wirkliche Attenuation. Subtrahiert man daher von der ersteren die letztere, so erhält man die Differenz beider."

[christianf]

Danke Oli,

oft werden die Dinge klarer, wenn man eine Formel etwas anders hinschreibt.

Gibt eigentlich irgendwo einen Standard für Formelzeichen in der Brauerei? Wenn ich mir so die verschiedenen Bücher und Stellen im Internet anschaue, scheint jeder etwas anderes zu machen.

Gruss, Christian

[§11]

Danke Oli,

oft werden die Dinge klarer, wenn man eine Formel etwas anders hinschreibt.

Gibt eigentlich irgendwo einen Standard für Formelzeichen in der Brauerei? Wenn ich mir so die verschiedenen Bücher und Stellen im Internet anschaue, scheint jeder etwas anderes zu machen.

Gruss, Christian

Dazu kommt das sich "Viele" einfach weigern die richtige Bezeichnungen zu verwenden. Siehe EVG für ein Bier das ausgestossen wird oder °P für die Angabe von Restextrakt. Ich hab einfach aufgegeben

Recht gut hat das Oli in der Hilfe seiner Software erklärt http://www.brewrecipedeveloper.de/

Gruss

Jan

[christianf]

°P für die Angabe von Restextrakt.

Das ist tatsächlich Unsinn, da das °P überhaupt nur für Würze definiert ist. Ich finde es aber auch physikalisch unschön bis unsinnig, wenn auf beiden Seiten einer Gleichung unterschiedliche Maßeinheiten stehen, also fände ich es sauberer auch die Stammwürze in Massen% anzugeben.

[Commander8x]

Gut ausgeführt finde ich das in den Veröffentlichungen der Professoren Manger und Annemüller.
Als Beispiel die "Berechnungen zur Würzeherstellung" aus der Zeitschrift BrauereiForum der VLB, Ausgabe 10/2019, S. 12-15.
Einen direkten Link gibt es leider nicht, man muss sich da etwas durchklicken.

Auch in ihrem Buch "Fachrechnen für Mälzerei- und Brauereitechnologen" ist das enthalten.

Gruß Matthias

[olibaer]

Auch in ihrem Buch "Fachrechnen für Mälzerei- und Brauereitechnologen" ist das enthalten.

Absolut, eine ganz wunderbare Lektüre.
Ich prüfe meine Rechenwege immer gegen dieses Standardwerk ab.

[olibaer]

Das ist tatsächlich Unsinn, da das °P überhaupt nur für Würze definiert ist. Ich finde es aber auch physikalisch unschön bis unsinnig, wenn auf beiden Seiten einer Gleichung unterschiedliche Maßeinheiten stehen, also fände ich es sauberer auch die Stammwürze in Massen% anzugeben.

Vielleicht hilft auch hier ein kleiner Perspektivwechsel:

Ins "Heute" übersetzt ist °P die Dimension für Würze und %w/w ist die zugehörige Einheit.
Wird aus Würze Bier, entfällt die Dimension °P für Würze. Übrig bleibt die Einheit %w/w.

[afri]

Ich bin dagegen. Habe ich bestimmt schon mal geschrieben.

Der Hobbybrauer taucht seine Spindel in die Würze nach dem Abkühlen, ermittelt z.B. 12°P und liegt damit genau im diskutierten Bereich von euch. Jetzt wird "der Zeug" gegeben und das Bier gärt zuende. Danach taucht der Hobbybrauer seine Spindel wieder ein und ermittelt z.B. 2°P. Darf er aber nicht mehr sagen, weil es jetzt %xmas oder so heißt. Finde ich doof, weil Brauer (mwd) seit vielen Jahren das genau so tun und damit vielleicht nicht exakt richtig liegen, aber wesentliche Werte so benannt werden können, die auch anders benannt nichts am Bier änderten.

Ja, ich habe den Artikel im Brau!Magazin gelesen und sogar korrigiert, aber an meiner Meinung ändert das nichts. Ich rechne meine Alkoholwerte nach wie vor mit Earls Refraktorechner aus, welches reale sowie scheinbare Werte ausgibt. Aber die realen scheren mich nicht, da nur die scheinbaren Werte seit langer Zeit interessant für mich sind. So wie es das für viele Generationen vor uns auch war. Ich sehe keinen Grund, das jetzt zu ändern, auch wenn es korrekter wäre. Siehe PS oder kW, beim Motorrad oder Auto rechnet doch auch vermutlich jeder noch in den alten und vertrauten Einheiten. Ebenso sehe ich das in diesem Punkt hier.
Achim

[christianf]

Gut ausgeführt finde ich das in den Veröffentlichungen der Professoren Manger und Annemüller.
Als Beispiel die "Berechnungen zur Würzeherstellung" aus der Zeitschrift BrauereiForum der VLB, Ausgabe 10/2019, S. 12-15.

Schöne Zusammenbestelllung, aber nur Rechnungen zur Würzebereitung. Ich habe mir die Ausgabe mal heruntergeladen.

[christianf]

Auch in ihrem Buch "Fachrechnen für Mälzerei- und Brauereitechnologen" ist das enthalten.

Absolut, eine ganz wunderbare Lektüre.
Ich prüfe meine Rechenwege immer gegen dieses Standardwerk ab.

Werden in diesem Buch denn die Formeln hergeleitet oder nur mitgeteilt?

[olibaer]

Der Hobbybrauer taucht seine Spindel in die Würze nach dem Abkühlen, ermittelt z.B. 12°P und liegt damit genau im diskutierten Bereich von euch. Jetzt wird "der Zeug" gegeben und das Bier gärt zuende. Danach taucht der Hobbybrauer seine Spindel wieder ein und ermittelt z.B. 2°P. Darf er aber nicht mehr sagen, weil es jetzt %xmas oder so heißt. Finde ich doof, weil Brauer (mwd) seit vielen Jahren das genau so tun ...

Genau das tut er eben nicht.
Fahr in eine Brauerei deiner Wahl und Frage den Brauer der gerade den Gärkeller "gradiert/durchspindelt", welchen "scheinbaren Restplatogehalt" er denn gerade ermittelt hat. Der wird dich anschauen wie eine Kuh wenns blitzt - garantiert.

[Sura]

*hust* .... dann sollte man da aber mal schnell drüberarbeiten:
https://hobbybrauer.de/forum/wiki/doku. ... ausrechnen.
https://hobbybrauer.de/forum/wiki/doku. ... erungsgrad

Narziss (und auch andere) bezeichnen den Restextrakt übrigens ganz einfach mit %. Das erscheint mit etwas eingängiger als das sperrige %w/w. Darauf kann man sich doch einfach einigen, oder? :)

Gruß,
Kai

[olibaer]

*hust* .... dann sollte man da aber mal schnell drüberarbeiten:
https://hobbybrauer.de/forum/wiki/doku. ... ausrechnen.
https://hobbybrauer.de/forum/wiki/doku. ... erungsgrad

Ja, diese Diskussion hatten wir schon öfter.

Zwischen dem scheinbaren Extrakt Es, dem wirklichen Extrakt Ew, dem Alkoholgehalt und der (ursprünglichen)Stammwürze P besteht eine rechnerische Beziehung, die Balling in seinen Attenuationslehren beschreibt - bekannt als Ballingformel.

Würden unsere Tools zwischen P und Es nicht unterscheiden, ginge jede berechnete Bieranalyse auf die Bretter.
Nur ein Grund, weshalb ein Messwert nach der Hefegabe(Gärung) nicht in der Einheit °P angegeben werden sollte.

Narziss (und auch andere) bezeichnen den Restextrakt übrigens ganz einfach mit %. Das erscheint mit etwas eingängiger als das sperrige %w/w.

Das ist nicht nur in Fachbüchern so üblich, sondern auch in der gelebten Praxis.
Eine festgestellte Extraktkonzentration wird in der alltäglichen Brauerkommunikation einfach in % angegeben und jeder weiß, was damit gemeint ist.

Ich wäre sofort dabei nur noch % zu verwenden und ich wüsste, dass es sich dabei - eigentlich, um eine auf 20°C korrigierte Saccharometeranzeige handelt. Wäre es eine Würzeprobe wüsste ich, dass mit % die Platograde P gemeint sind, bei einer Gärprobe wüsste ich, dass mit % der Extrakt scheinbar Es gemeint ist.

So schließt sich der Kreis zwischen P, Es und % ;-)

Nicht zu vergessen, dass der Hobbybrauer mittlerweile drei unterschiedliche Meßprinzipien am Start hat: Archimedes, Brechungsindex, Schall.
Letzen Endes müssen die physikalischen Grundlagen dieser Meßprinzipien zum Probenkontext bekannt sein, damit man mit % noch etwas anfangen kann ... das sieht für hier nicht gut aus.

Unter uns:
Es ist doch heute schon so, dass zur Beantwortung von einfachen Fragen zunächst & gefühlt fünf Nachfragen notwendig sind, um überhaupt zu verstehen, was angefragt wird. Ein Teil des Problems ist, dass Einheiten nicht mitgeführt, nicht angegeben oder falsch verstanden werden - man ganz klassisch, aneinander vorbeiredet. Ich denke wir werden noch ein wenig Zeit brauchen, bis alleine % im Kontext richtig verstanden wird ;-)

[olibaer]

Hallo Christian,

In der genaueren Balling-Formel steckt auch noch drin, dass ein kleines bisschen Masse durch CO2 und Hefe verloren geht, aber das dürfte bei dieser Ableitung keine Rolle spielen.

Während der Bearbeitung von #13 und #14 ist mir der Eingangspost #1 mit dem Zitat von oben vor die Füße gefallen:
"Das kleines bisschen Masse das durch CO2 und Hefe verloren geht, das dürfte bei dieser Ableitung keine Rolle spielen".

Und ob es das tut - und wie. Hier zum Einstieg die Formel für den Ew:

Ew% = 0,1808 · P + 0,8192 · Es

Die Formel beschreibt ein Potential für einen Ew, nicht aber in welcher Masse Bier sich dieses Potential am Ende der Vergärung aufkonzentriert. Balling hat genau dieses Thema aufgegriffen und entlang seiner Attenuationslehren die Ballingformel ersonnen.

In aller Kürze kann ich das jetzt nicht erklären, aber nehmen wir mal 100 g Würze mit 12,0 °P und einem Es von 2,4% an.
Ausgerechnet werden soll, welche Masse Bier in g am Ende einer Würzevergärung übrig bleibt:

g Bier = 100 - ((P-Es)*0,4228) = 95,94 g

Aus 100 g Würze entstehen am Ende der Gärung 95,94 g Bier. Wenn man so möchte - Ballingschwand.
Ew% nach der Formel oben und mit den Beispielwerten für P und Es berechnet:

Ew% = 0,1808 · 12 + 0,8192 · 2,4 = 4,14%

Aus 100 g Würze sind 95,94 g Bier entstanden. Der für die Würze berechnete Ew% ergibt sich für "Bier" neu zu:
Ew% = 4,14 / 95,94 * 100 = 4,31%

4,31 zu 4,14 im Ew% sieht nach wenig aus, aber Vergleichbares geschieht mit dem Potential für Alkohol. Nimmt man Beides zusammen, zeigt die Rückrechnung der Stammwürze via Ballingformel die Unterschiede auf: falsch 11,5°P / richtig 12,0°P.


Hier ist definitiv ein Clown mehr im Zelt.
Ein kleines bisschen Masse durch CO2 und Hefe verloren - das ist zu genügsam. ;-)

[maxifranke]

Die Differenz zwischen scheinbarem und wirklichem Extrakt ergibt sich ja dadurch, dass der bei der Gärung entstandene Alkohol die Dichtemessung beeinflusst. Der mit einem reinen Dichtemessgerät (z.B. Spindel, Refraktometer oder Biegeschwinger) nach oder während der Gärung ermittelte Extrakt enthält also einen "Alkoholfehler".

Dieser Messfehler ist in der Praxis natürlich immer ungefähr gleich. Deshalb kann für Berechnungen im Betriebsalltag der wirkliche Vergärungsgrad aus dem scheinbaren Vergärungsgrad mit dem Faktor 0,81 berechnet werden.

Vw = 0,81 * Vs

Aus der Stammwürze und dem wirklichen Vergärungsgrad ergibt sich dann der wirkliche Extrakt.

Ew = P-(P * Vw)/P
Wenn man in Prozenten gerechnet hat, muss natürlich noch ein Faktor 100 mit einbezogen werden.

Will man den wirklichen Extrakt genau bestimmen, kommt man nicht umhin den Alkoholgehalt direkt zu bestimmen. Dies kann z.B. mittels Destillation, Nahinfrarotspektroskopie oder Schallgeschwindigkeitsmessung erfolgen.

Zum Thema CO2-Bildung:
Über den Daumen gepeilt kann man sagen, dass aus der Stammwürze nach der Gärung ca. 1/3 Alkohol, 1/3 CO2 und 1/3 Restextrakt (wirklich) geworden ist. Aus einer P12 Würze sind somit also ca. 40 g CO2/kg Würze entstanden. Mithin lösen sich also ca. 4% des Asugangsgewichtes buchstäblich in "Luft" auf. Das ist schon eine ganze Menge.

[olibaer]

Aus der Stammwürze und dem wirklichen Vergärungsgrad ergibt sich dann der wirkliche Extrakt.

Ew = P-(P * Vw)/P

Wenn man in Prozenten gerechnet hat, muss natürlich noch ein Faktor 100 mit einbezogen werden.

Magst über die Formel nochmal drüberschauen? Das passt so nicht.
Beispiel 01:

P = 12,0 %
Vw = 65,0 %

Ergibt nach der Formel von oben für den Ew %:
Ew = 12-(12 * 65)/12 = - 54 %

Auch wenn ich den Faktor 100 mit einbeziehe, kommt da nichts Gutes dabei heraus - es wird nur anders falsch.
So denke ich wirds' richtig:

Ew = P - (P * Vw) / 100

... aber auch nicht ganz. Siehe meine Anmerkungen dazu im Beitrag #15

Wenn du für das Beispiel 01 einen Extrakt wirklich Ew[%] zu 4,38 % berechnest, dann hats gepasst

[olibaer]

Hallo Christian, hallo zusammen,

mir ist dieser Beitrag neulich wieder vor die Füsse gefallen.
Im Eingangspost hinterfragst du die Herkunft für die verbreitete Formel für den Extrakt wirklich Ew:

... ich versuche gerade die verschiedenen Formeln ums Brauen zu verstehen und die meisten lassen sich ja auch aus einfachen physikalischen Zusammenhängen elementar ableiten. Beim Zusammenhang zwischen dem scheinbaren Restextrakt und dem tatsächlichen Restextrakt stecke ich allerdings fest.

Die Formel für den tatsächlichen Restextrakt, die überall mitgeteilt, aber nie begründet wird, lautet (***)

Er = 0,8192 · Es + 0,1808 · Eo

(E steht bei mir für Extrakt und die Indizes r für "Rest", s für "scheinbar" und o für "original", also für die Stammwürze.)

Geschrieben/publiziert wird die Formel für den Ew mehrheitlich so.

Formel 01:

Ew = 0,8192 x Es + 0,1808 x P

• Ew = Extrakt wirklich [%]
• Es = Extrakt scheinbar [%]
• P = Stammwürze [%]

Erneut hab' ich mich auf die Suche nach Quellen gemacht, die diese Formel für den Ew zusammenhängend erklären oder gar herleiten.
Ergebnis: Fehlanzeige!
Selbst ist der Brauer, und manchmal auch etwas trotzig: dann mach' ich es eben selbst.

Hier die Herleitung für Formel 01:

Los gehts mit einer Kernaussage aus den Ballingschen' Attenuationslehren. Zitat 01[1]:

"Dieser Attenuationsquotient zeigt daher an, um wie vielmal die scheinbare Attenuation größer ist als die wirkliche"

Diesen Attenuationsquotienten den Balling beschreibt, der liegt aktuell bei: 1,2207
Ob dem so ist, das hab' ich mit ein paar Echtdaten aus dem HBCON-Labor überprüft:

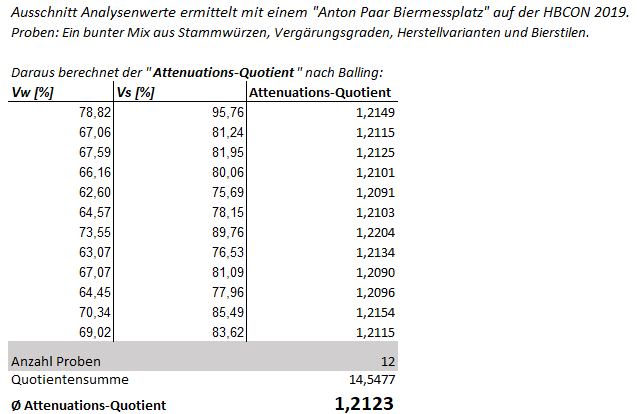
Berechnung Attenuationsquotient aus Vs und Vw

attenuationsquotient_berechnetausechtdaten.PNG (20.38 KiB) 3640 mal betrachtet

Kommt hin.

Jetzt ist der Attenuationsquotient 1,2207 in der Brauermathematik nicht wirklich verbreitet, sein Gegenpart, der Ballingsche' Attenuationsfaktor 0,8192 , hingegen schon. Um dort hinzukommen, müssen wir die Aussage von Balling (Zitat 01) ins Gegenteil verkehren und begleitend dazu den Kehrwert aus dem Attenuationsquotient bilden:

"Dieser Attenuationsfaktor zeigt daher an, um wie vielmal die wirkliche Attenuation kleiner ist als die scheinbare"
Ballingsche' Attenuationsfaktor = 1/1,2207 = 0,8192

Der Zusammenhang zwischen wirklich und scheinbar ist hergestellt. Was noch bleibt ist der Rückschluss auf eine nicht vergorene Extraktmenge Ew aus den Angaben zu einer scheinbaren Extraktkonzentration Es und den Angaben zu einer ursprünglich vorhandenen Extraktkonzentration. Der Stammwürze P.

Für den nötigen Durchblick sorgt die Betrachtung einer scheinbar vergorenen Extraktmenge, einer wirklich vergorenen Extraktmenge und die Differenz dieser beiden Werte. Die Differenz dieser beiden Werte beschreibt das, was uns als "Alkoholfehler" bekannt ist. Balling bringt es ein weiteres mal' auf den Punkt. Zitat 02[2]:

"Der Verlust an der Dichte der gährenden Flüssigkeit während ihres Gährungsverlaufes hat zwei sich bedingende Ursachen, nämlich einmal: das Verschwinden des Zuckers aus derselben durch sein zerfallen in Alkohol und Kohlensäure, und zweitens: die Bildung von Alkohol, eines Körpers, welcher spezifisch leichter ist als Wasser."

Die scheinbar vergorene Extraktmenge ist
Formel 02:

vEs[%] = P[%] - Es[%]
Beispiel: P=12, Es=2 -> vEs = 10


Die wirklich vergorene Extraktmenge ist
Formel 03:

vEw[%] = P[%] - Ew[%]
Beispiel: P=12, Ew=4 -> vEw = 8


Der Extrakt wirklich Ew ist uns zumeist unbekannt, weswegen sich vEw[%] nicht so einfach berechnen lässt. Hier hilft der Ballingsche' Attenuationsfaktor 0,8192 weiter.

Die wirklich vergorene Extraktmenge ist
Formel 04:

vEw[%] = vEs[%] x 0,8192
Beispiel: vEs=10, vEw=10 x 0,8192


Die Formel 04 bringt die Abhängigkeit zwischen einer scheinbar vergorenen Extraktmenge und einer wirklich vergorenen Extraktmenge auf den Punkt. Übersichtlicher schauts so aus.
Formel 05:

vEs x 0,8192 = vEw


Um jetzt wieder die Stammwürze P und den Extrakt wirklich Ew ins Spiel zu bekommen, wird vEs durch "P-Es"(Formel 02) ersetzt und vEw durch "P-Ew"(Formel 03).
Formel 06:

(P-Es) x 0,8192 = P-Ew


Im letzten Schritt der Herleitung wird die Formel 06 nach dem gesuchten Extrakt wirklich Ew aufgelöst.
Klammern entfernen:
0,8192 x P - 0,8192 x Es = P - Ew

Nach Ew umstellen:
Ew = P - 0,8192 x P + 0,8192 x Es

Segment P - 0,8192 x P behandeln:
1 x P - 0,8192 x 1 x P -> (1 - 0,8192) x P -> 0,1808 x P

Segment einsetzen/Lösung:
Ew = 0,1808 x P + 0,8192 x Es


P.S.: Nicht alle Lösungsschritte für den gesuchten Extrakt wirklich Ew sind hier dokumentiert. Bitte bei Bedarf die Formel 06 selber nach Ew auflösen oder auflösen lassen.

Zusammenfassung:
Die Grundlage für die Formel Ew = 0,8192 x Es + 0,1808 x P ist die Abhängigkeit zwischen einer scheinbar vergorenen Extraktmenge vEs und einer wirklich vergorenen Extraktmenge vEw, die nach den Ballingschen' Attenuationslehren in folgender Beziehung besteht:
vEs x 0,8192 = vEw
oder
vEw x 1,2207 = vEs

Hinweis für alle Selbstrechner, Bieranalytiker und Softwareentwickler!
Der über die Formel Ew = 0,8192 x Es + 0,1808 x P berechnete Extrakt wirklich ist nicht der Extrakt wirklich, der sich final im Bier einstellt. Vielmehr wird durch den Ergebniswert beschrieben, welches Potenzial für den Extrakt wirklich in der Würze steckt. In welcher Menge Bier er sich am Ende der Herstellung aufkonzentriert, das bleibtin der Formel unberücksichtigt. Siehe hier #15.


Quellen:
[1] Balling, Carl Joseph Napoleon: Die Gährungschemie wissenschaftlich begründet und in ihrer Anwendung auf die Bierbrauerei, Branntweinbrennerei, Hefenerzeugung, Weinbereitung und Essigfabrikation practisch dargestellt, Band 1, S.203, Verlag F. Tempsky, Prag 1845; Abgerufen am 05.08.2023

[2] Balling, Carl Joseph Napoleon: Die Gährungschemie wissenschaftlich begründet und in ihrer Anwendung auf die Bierbrauerei, Branntweinbrennerei, Hefenerzeugung, Weinbereitung und Essigfabrikation practisch dargestellt, Band 1, S.189, Verlag F. Tempsky, Prag 1845; Abgerufen am 05.08.2023

[emjay2812]

Ich als mathematischer Laie verstehe da nur Bahnhof.

Warum ändert sich den plötzlich bei gärender Würze die Maßeinheit von °P auf %? Meiner Meinung nach geht es um den Zuckergehalt,
der mit laufender Gärung absinkt. Meine Würze hat also am Anfang 13°P, mein Jungbier dann plötzlich am Ende der Gärung 3%?

Mach für mich keinen Sinn.

[renzbräu]

°P sind Gewichts-% in g, werden aber nur für die Stammwürze verwendet. Sobald die Gärung einsetzt, ist es aber nicht mehr die Stammwürze. Man bleibt somit in der selben Dimension.

[Ladeberger]

Vielen Dank Oli für diese Tiefbohrung, etabliertes Fachrechnen auch mal fundiert hinterfragt, wunderbar. Die perfekte Lektüre zum Sonntagmorgen bei einem großen Pott Kaffee!

Gruß
Andy

[Commander8x]

Warum ändert sich den plötzlich bei gärender Würze die Maßeinheit von °P auf %? Meiner Meinung nach geht es um den Zuckergehalt,
der mit laufender Gärung absinkt. Meine Würze hat also am Anfang 13°P, mein Jungbier dann plötzlich am Ende der Gärung 3%?

Die Plato-Einheit umfasst den gesamten Restextrakt (alle aus dem Malz gelösten Stoffe), der nach dem Maischen in Lösung gegangen ist. Der Vergärungsgrad und Restextrakt bezieht sich dagegen nur noch auf den Zuckergehalt (Masse-%).

Gruß Matthias

[emjay2812]

Und was misst meine Spindel?

[Colindo]

Die Plato-Einheit umfasst den gesamten Restextrakt (alle aus dem Malz gelösten Stoffe), der nach dem Maischen in Lösung gegangen ist. Der Vergärungsgrad und Restextrakt bezieht sich dagegen nur noch auf den Zuckergehalt (Masse-%).

Das ist nicht korrekt, beides bezieht sich auf alle Stoffe und (Masse-)% ist immer die richtige Einheit. °P wird nur ausnahmsweise für die Stammwürze benutzt. Alles andere bleibt in %.

[olibaer]

Und was misst meine Spindel?

Das Messprinzip ist die Dichtebestimmung. Der Messwert einer Bier- oder Würzespindel ist das Dichteäquivalent einer wässrigen Saccharoselösung bei gleicher Temperatur. Der Ablesewert hingegen ist immer in Zusammenhang mit der vom Hersteller angegebenen Einheit zu verstehen, die sich zumeist angedruckt auf der Rückseite der Skalenfolie im Spindelhals befindet.

Je nach Hersteller findet man hier für Bier- oder Würzespindeln:

• %mas
• mas%
• °P
• Massenprozent-%
• GG-%

[Sebasstian]

Ich als mathematischer Laie verstehe da nur Bahnhof.

Warum ändert sich den plötzlich bei gärender Würze die Maßeinheit von °P auf %? Meiner Meinung nach geht es um den Zuckergehalt,
der mit laufender Gärung absinkt. Meine Würze hat also am Anfang 13°P, mein Jungbier dann plötzlich am Ende der Gärung 3%?

Mach für mich keinen Sinn.

Die Frage hatte Oli hier oben schonmal ganz gut beantwortet vor langer Zeit:

Das ist tatsächlich Unsinn, da das °P überhaupt nur für Würze definiert ist. Ich finde es aber auch physikalisch unschön bis unsinnig, wenn auf beiden Seiten einer Gleichung unterschiedliche Maßeinheiten stehen, also fände ich es sauberer auch die Stammwürze in Massen% anzugeben.

Vielleicht hilft auch hier ein kleiner Perspektivwechsel:

Ins "Heute" übersetzt ist °P die Dimension für Würze und %w/w ist die zugehörige Einheit.
Wird aus Würze Bier, entfällt die Dimension °P für Würze. Übrig bleibt die Einheit %w/w.

[christianf]

Danke Olibaer :). ich werde deine Rechnung demnächst mal nachvollziehen.

[Print]

Zufällig bin ich auf dieses Forum gestossen und möchte Euch meine eigene Herleitung dieser Näherungsformel nicht vorenthalten:

Verbesserte Näherung für die Berechnung des wirklichen Restextraktes aus der Stammwürze und dem scheinbaren Restextrakt

Symbole:
p Stammwürze in °P (= %mas = g/100g)
Es Scheinbarer Restextrakt in %mas
Ew Wirklicher Restextrakt in %mas
q Balling-Faktor, dimensionslos *)
Vs Scheinbarer Vergärungsgrad in %
Vw Wirklicher Vergärungsgrad in %

Exakte Berechnung des wirklichen Restextraktes nach Balling:

Ew = (p * q + Es) / (1+q) mit q = 0.220 + (p / 1000) *)

beziehungsweise

Ew = p * [q / (1 + q)] + Es * [1 / (1 + q)]

Berechnet man den Faktor q in dieser Formel für eine Stammwürze p von 0°P
(genau: 0.7°P), so ergibt sich die in unzähligen Quellen publizierte Näherungsformel:

q = 0.220 + [0.7 / 1000] = 0.2207
Ew = p * [0.2207 / 1.2207] + Es * [1 / 1.2207]

Ew = p * 0.1808 + Es * 0.8192

Das heisst also, diese Näherungsformel stimmt nur genau für eine Stammwürze von 0.7°P und zeigt bei allen realen Stammwürzen eine Abweichung.
Die maximale Abweichung dieser Formel von der exakten Berechnung von Ew für Stammwürzen von 6-22°P und Restextrakte von 1-6 %mas beträgt 0.295 %mas

Besserer Ansatz:

Exakte Berechnung für eine Stammwürze von 12°P => q = 0.220 + (12 / 1000) = 0.232

also:

Ew = p * [0.232 / 1.232] + Es * [1 / 1.232]
Ew = p * 0.1883 + Es * 0.8117

Diese Formel stellt für den praktischen Bereich eine bessere Näherung dar und ist bei einer Stammwürze von 12°P sogar exakt!
Die maximale Abweichung dieser Formel von der exakten Berechnung von Ew für Stammwürzen von 6-22°P und Restextrakte von 1-6 %mas beträgt 0.137 %mas
In Analogie dazu gilt als Näherungsformel für die Berechnung des wirklichen Vergärungsgrades aus dem scheinbaren Vergärungsgrad:

Vw = Vs * 0.8117


*) Berechnet nach Pawlowski/Schild: Die Brautechnischen Untersuchungsmethoden, 8. Auflage, Seite 247:
q = 0.220 + (p /1000)

Anmerkung:
Im Gegensatz dazu ist der im Originalwerk: Balling-1845-Gährungschemie-Band 1 auf Seite 202 definierte und in der Ausgabe von 1854 in der Tabelle XII aufgeführte «Attenuationsquotient q» um 1 grösser als der oben berechnete Wert, also
qBALLING = 1.220 + (p /1000)

Mit wohlgehopften Grüssen
Print

[olibaer]

Hallo Print,

Ew = p * 0.1883 + Es * 0.8117

Diese Formel stellt für den praktischen Bereich eine bessere Näherung dar und ist bei einer Stammwürze von 12°P sogar exakt!

Ich hab mit deiner Variante für Ew ein Beispiel aufgebaut und eine kleine Bieranalyse gerechnet:

P% = 12
Es% = 3
Ew% = 4,69
Alc. %w/w = (12 - 4,69) * 0,4839 = 3,54

Hint 0,4839: Aus 1 g vergärbarer Extraktmenge entsteht 0,4839 g Alkohol

Prüfung:
Setzt man die berechneten Werte für Ew und für Alc. in die Ballingformel ein, dann müsste sich daraus die in Ansatz gebrachte Stammwürze P = 12 ergeben:

P = (3,54 * 2,0665 + 4,69)/(3,54*1,0665+100)*100 = 11,56


Zur besseren Übersicht. Mein Beispiel in Excel:

EwUndBAneu.PNG (9.21 KiB) 2429 mal betrachtet

Vielleicht prüfst du deinen Lösungsansatz für Ew nochmal.
Zwischen 11,56 IST und 12,00 SOLL ist noch Luft nach oben.

[Print]

Hallo Oli,

Nach Auflösung der grossen Ballingschen Stammwürzeformel nach A ergibt sich:

A %mas = (p - Ew) / [ 2.0665 - (1.0665/100) * p]

Den Ausdruck
1 / [ 2.0665 - (1.0665/100) * p] hat Balling als Faktor b bezeichnet und tabelliert (siehe Anhang), also gilt

A %mas = b * (p - Ew)

somit ergibt sich in unserem Beispiel für p = 12%mas und Ew = 4.69%mas:

b = 0.51586 und damit wird

A = 0.51586 * (12 - 4.69) = 3.77 %mas

Eingesetzt in die Ballingformel
p = (A * 2.0665 + Ew) * 100 / (100 + A * 1.0665)
ergibt sich für die Stammwürze:

p =(3.77 * 2.0665 + 4.69) * 100 / (100 + 3.77 * 1.0665) = 12°P

q.e.d.

Mit wohlgehopftem Gruss
Print

[olibaer]

Hallo Print,

so lässt sich aber nicht überprüfen, ob

Ew = p * 0.1883 + Es * 0.8117

richtig ist, wenn Du in der Herleitung den eigentlich zur Überprüfung gesuchten Wert P als bekannt annimmst.

Hier:
1 / ( 2.0665 - (1.0665/100) * p)

und hier
A %mas = b * (p - Ew)

Beispielsweise könnte ich diese Formel für den Ew ersinnen:
Ew = P * 0.1 + Es * 0.9

Für P = 12 und Es = 3 ergibt sich
Ew = 12,0 * 0,1 + 3 * 0,9 = 3,9

Deine Berechnung für A %mas übernehme ich mit Ew von oben(3,9). b(0.51586) bleibt bei gleicher Stammwürze unverändert:
A = 0.51586 * (12 - 3,9) = 4.18 %mas


Die Ergebnisse für Ew und A setze ich in die Ballinghformel ein:
p =(4.18 * 2.0665 + 3.9) * 100 / (100 + 4.18 * 1.0665) = 12°P

Obwohl ich zur Berechnung von Ew irgendwelchen VooDoo erfunden habe, kommt mit Deiner Art P zu überprüfen trotzdem 12 raus.
Wie von Dir hergeleitet kommt für jeden Ew zwischen >=0 und Ew <=12 immer eine Stammwürze von 12 raus.

Die Überprüfung der Methode ist erst dann valide, wenn A %mas ohne die Kenntnis von P ermittelt wird.

Gruß
Oli

[Print]

Hallo Oli,

Ich wollte nur zeigen, dass aus der korrekten Berechnung des Alkoholgehaltes auch eine korrekte Stammwürze (ohne «Luft nach oben») resultiert. Es handelt sich keinesfalls um einen Beweis für die "Richtigkeit" meiner Methode und mir ist auch klar, dass aus dem aufgezeigten Berechnungsgang für alle Ew = p * m + Es * n, welche die Bedingung: m + n = 1 erfüllen, identische Werte für p resultieren, was ich aber für meine ursprüngliche Absicht als nicht relevant erachte:
Was ich mit meinem Beitrag #28 eigentlich aufzeigen wollte, ist die Tatsache, dass die allgemein verbreitete Näherungsformel für Ew noch fast nie gründlich hinterfragt wurde und noch ein gewisses Verbesserungspotential hat, weshalb ich sie neu herleite und einen Vorschlag für eine verbesserte Formel präsentiere, welche im Bereich der normal üblichen Stammwürzewerte etwas genauer und für 12°P sogar exakt ist.

Da es sich aber um eine Näherungsformel handelt, ist sie weder richtig noch falsch, sondern nur genauer oder ungenauer, d.h. ihre Gültigkeit lässt sich praktisch nicht formal, sondern nur numerisch nachweisen.

Deshalb möchte ich die von Dir gewünschte «Validierung der Methode» ganz pragmatisch in Form einer Tabelle präsentieren, ohne dabei mathematisch weniger interessierte Forumsbesucher weiterhin mit unzähligen Formeln und Herleitungen zu langweilen.
(die Berechnung der exakten Stammwürze in der Tabelle erfolgt gemäss meinem Beitrag #28)

So kann sich jeder ein eigenes Bild machen und selber entscheiden, ob er die vorgeschlagene Näherungsrechnung für Ew übernehmen will.

Tabelle Ew aus p und Es.pdf

(52.3 KiB) 53-mal heruntergeladen

Abschliessende Bemerkung:
Offensichtlich bin ich nicht der Erste, der auf diese Idee kam: Vor Kurzem bin ich auf einen Artikel von 1995 von Michael Hall im «Zymurgy» - dem legendären Magazin der US-Homebrewer - gestossen, in dem er einen ähnlichen Vorschlag zur Verbesserung der Näherungsformel für Ew (engl. RE) macht.

Zitat auf Seite 57, oben links:
«Fortunately, Balling once again comes to the rescue with an empirical relationship between the real extract, the apparent extract and the original extract:
q = 0.22 + 0.001 OE RE = (q OE + AE) / (1 + q)
The variable q is called the attenuation coeffcient, but you can just think of it as an intermediate value. Many sources quote this equation in the form RE = 0.8192 AE + 0.1808 OE, but this form assumes that q is calculated at an OE of zero, which is not very accurate.
For our simplifed version, we’ll calculate q assuming a reasonable OE of 12.5 °P, which gives us
RE = 0.8114 AE + 0.1886 OE»

Link zum Artikel:
https://www.homebrewersassociation.org/ ... Zym95.pdf


Mit wohlgehopftem Gruss
Print

[olibaer]

Hallo Print,

saubere Arbeit und toll recherchiert. Ich könnte mich reinlegen. Danke dafür :-)

Deshalb möchte ich die von Dir gewünschte «Validierung der Methode» ganz pragmatisch in Form einer Tabelle präsentieren, ohne dabei mathematisch weniger interessierte Forumsbesucher weiterhin mit unzähligen Formeln und Herleitungen zu langweilen.

Full ACK!

Am Formelwerk
Ew = P * 0.1808 + Es * 0.8192
lässt sich bestimmt optimieren. Aber:

Der eigentliche Hack ist, dass der so oder ähnlich berechnete Ew das Potenzial aus Sicht einer Anstellwürze beschreibt.
Endvergoren sind wir aber im "Bier" und auf dem Weg Würze->Bier ist Masse verloren gegangen(Hefe, CO2).

Beispielsweise bleiben, bei einem Vergärungsgrad von 80%, von 100 g Anstellwürze nur noch ~ 96 g Bier übrig (Ballingschwand).
In Entsprechung konzentriert sich eine verbliebene Extraktmenge(Ew) oder eine für die Würze berechnete Alkoholmenge nicht in 100 g Würze auf, sondern in 96 g Bier.

Bevor berechnete Werte für Ew oder Alkohol in die Ballingformel eingesetzt werden, müssen sie zunächst von 96 g Bier auf 100 g Würze zurückgerechnet werden. Bleibt die Rückrechnung im Kontext einer Bieranalyse aus, dann spielt die 4. Nachkommastelle in der Ew-Berechnung ohnehin keine Rolle mehr.

[Print]

Hallo Oli,

Danke für die Blumen

Mir persönlich ist die Alkoholberechnung nach Balling genau genug, insbesondere seit ich einen sehr starken Barley Wine (p = 24.40 °P, Es = 0.44 %mas)
bei einem Freund auf seinem Alex 500 von Paar analysieren liess.
Resultat der Analyse: 13.78 vol% alc. , berechnet: 13.50 vol% alc.

Hinsichtlich dem Fragenkomplex zur genaueren Berechnung des Alkoholgehalts kann ich Dir die ausführliche Publikation von Cutaia:
"Examination of the Relationships Between Original, Real and Apparent Extracts and Alcohol in Pilot Plant and Commercially Produced Beers"
sehr empfehlen, falls Du diese noch nicht kennst.

Hier 2 mögliche Links zur Publikation von Cutaia:

https://onlinelibrary.wiley.com/doi/epd ... tb00387.x

https://www.academia.edu/4189634/Examin ... uced_Beers

Mit wohlgehopftem Gruss
Print